Etape 1 - éléments de contexte
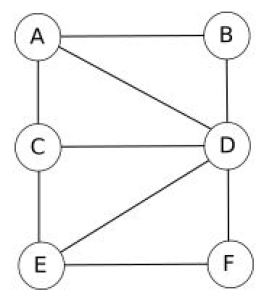
Imaginez un réseau social ayant 6 abonnés (A, B, C, D, E et F) où :
A est ami avec B, C et D
B est ami avec A et D
C est ami avec A, E et D
D est ami avec tous les autres abonnés
E est ami avec C, D et F
F est ami avec E et D
La description de ce réseau social, malgré son faible nombre d'abonnés, est déjà quelque peu complexe, alors imaginez cette même description avec un réseau social comportant des millions d'abonnés ! Il existe un moyen plus mathématique pour représenter ce réseau social : le graphe.
Ci-contre se trouve la représentation sous forme de graphe du réseau social décrit ci-dessus.
Dans un graphe, on représente chaque abonné par un cercle (avec le nom de l'abonné situé dans le cercle) et chaque relation "X est ami avec Y" par un segment de droite reliant X et Y ("X est ami avec Y" et "Y est ami avec X" étant représenté par le même segment de droite).
Les cercles sont appelés des sommets et les segments de droites des arêtes.
On peut alors exploiter cette représentation mathématique pour optimiser le fonctionnement de ce réseau social notamment en identifiant des acteurs centraux à privilégier pour diffuser de l'information.